Day 20 Magnetic Field

Today we began focusing on a new topic, the second portion of the electromagnetic field, magnetism.

A magnet pin controlling a compass

We first started class by Prof Mason demonstrating just what a magnetic field is by having a magnetized pin around the compass and moving the magnetic pin. We notice that the north side is following the magnetic pin

A discovery of how magnets work

We found out that magnets contain a north pole and a south pole, with the opposite attracting each other and the same repelling each other (just like how a proton and electron works)
We also see that if you cut a magnet in half, the ends of those sides become south and north respectively, meaning that it is impossible to have a single north/south side, otherwise known as a magnetic mono-pole

A Maxwell Equation, the integral of B (magnetic field) dA = 0 shows that there is no such thing as a magnetic monopole

Magnetic Flux

We then go on to study about magnetic flux and the similarities between a magnetic flux and a electric flux

Experimentation on exertion of electric charge

We then go over to see whether or not we can exert force on electrical charges that are moving by using a magnet, and the electron beam of an oscilloscope. 

More on the experimentation

We find out that once we move the magnet closer to the oscilloscope electron beam, the beam moves over to the left, showing us that the magnetic moves perpendicular to the beam, and therefore the magnetic force is both perpendicular to the direction of the magnetic flux and the moving charge

Equation proving what we saw

The right-hand rule

We then learned about the right-hand rule, and how important it is to understand how it works so that we can get an idea of where the Force and the Magnetic Field's direction is going

Back-stepping

Learning about the right-hand rule, we can go back to what we saw from the electron beam, and figure out where the force is pointing, which in this case, the force is pointing into the board

The next following picture are class examples in which we focused on learning and understanding more about the right hand rule

Example 1

Example 2 

Deriving radius in magnetism

By using what we know about magnetic force, within a circular region, we are able to then derive an equation for the radius of said region

The next few photos cover over the idea of rotation, primarily omega (angular velocity) and an example problem with it 

Electric field on a current carrying wire

We then studied the magnetic force of a current carrying wire understand the nature of a non-magnetic wire placed in a permanent magne

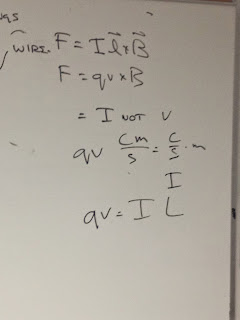Deriving another formula for magnetic field

We learned from the experimentation that there is indeed a magnetic force of the wire when the wire starts carrying current, and both the length and the current are perpendicular to the magnetic field, which gives us a second equation for magnetic force = ILxB, where I is the current, L is the length, and B is the magnetic field

Add caption

To get more of a grasp of how the magnetic field and force works, we were given a system where the magnetic field's direction is known, and asked where the magnetic force is point at each instance

We learned that the magnetic force only point when the magnetic field is parallel to the points shown, therefore only B and D are shown to have a force, pointing inside and outside respectively.